各向异性协方差矩阵与旋转和缩放矩阵#

用RS矩阵表示协方差矩阵#

论文中使用如下公式表示协方差矩阵：

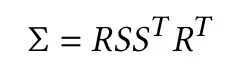
原因：任何高斯分布都可以用标准高斯分布通过仿射变换得到（反过来即是标准化），一维高斯分布使用μ和σ表示，多维使用μ和Σ（协方差）表示，由于有

假设x为标准高斯分布，则w中的Σ实际上就是单位阵I，则得到的w的协方差实际上就是：

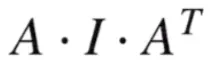
由于矩阵A是旋转矩阵R和缩放矩阵S的乘积，所以最终有

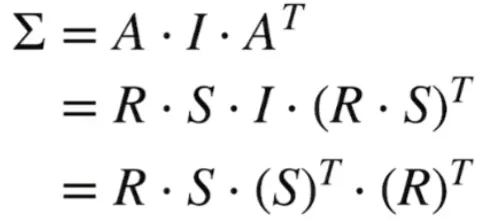
通过协方差矩阵求RS矩阵#

使用特征值分解

雅可比矩阵解决3d gaussian的投影变换#

在透视投影的渲染的过程中，光栅化之前需要经过相机变换、投影变换和视口变换，在经典情况下只需要求得model view projection（mvp）矩阵即可作用于整个空间中的物体，由于上文中高斯分布形成的椭球只有在仿射变换时才能保持其依然为高斯分布，而传统的投影变换却不是仿射变换，会导致协方差矩阵变形，因此需要寻找解决方式。

论文使用雅可比矩阵解决了这一问题，通过雅可比矩阵能够理解为在椭球核附近较小区域内对非线性变换的局部线性近似，因此可以利用其实现对仿射变换的模拟，得到

其中雅可比矩阵为：

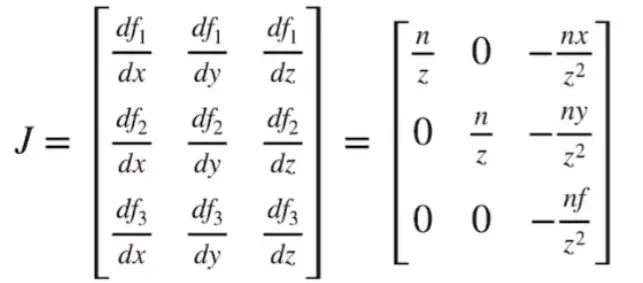
事实上就是对投影变换矩阵的求导。

将先前相机变换的结果带入得到：

需要注意的是，均值μ是做了传统的投影变换去到了222的立方体中，但是协方差矩阵是被压缩到[l, r][b, t][f, n]的长方体内（仅将锥体变换为柱体），因此之后μ需要做视口变换而协方差矩阵不用。

其他主要部分用到的技术#

机器学习优化#

随机梯度下降（GSD）#

从样本中随机抽出一组，训练后按梯度更新一次，然后再抽取一组，再更新一次，在样本量及其大的情况下，可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。（重点：每次迭代使用一组样本。）

为什么叫随机梯度下降算法呢？这里的随机是指每次迭代过程中，样本都要被随机打乱，这个也很容易理解，打乱是有效减小样本之间造成的参数更新抵消问题。

对于权值的更新不再通过遍历全部的数据集，而是选择其中的一个样本即可。一般来说其步长的选择比梯度下降法的步长要小一点，因为梯度下降法使用的是准确梯度，所以它可以朝着全局最优解（当问题为凸问题时）较大幅度的迭代下去，但是随机梯度法不行，因为它使用的是近似梯度，或者对于全局来说有时候它走的也许根本不是梯度下降的方向，故而它走的比较缓，同样这样带来的好处就是相比于梯度下降法，它不是那么容易陷入到局部最优解中去。

论文中的随机梯度下降的随机就在于每次采样的相机视角是随机的且每次迭代只考虑一个相机视角。

损失函数#

论文中用到的是L1 Loss和D-SSIM Loss (Data SSIM)

L1 Loss(MAE): 指模型预测值f (x)和真实值y之间绝对差值的平均值

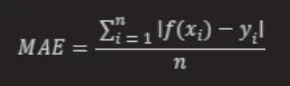
其中，f(xi) 和 yi 分别表示第 i 个样本的预测值及相应真实值，n 为样本的个数

D-SSIM Loss: SSIM是一种衡量重建图像和原图的相似性的尺度，D-SSIM是能直接运用于Data（浮点仿真数据）而不需要创建图像的一种方式

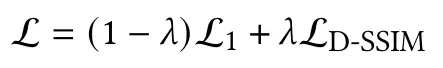
λ=0.2 in the test

激活函数#

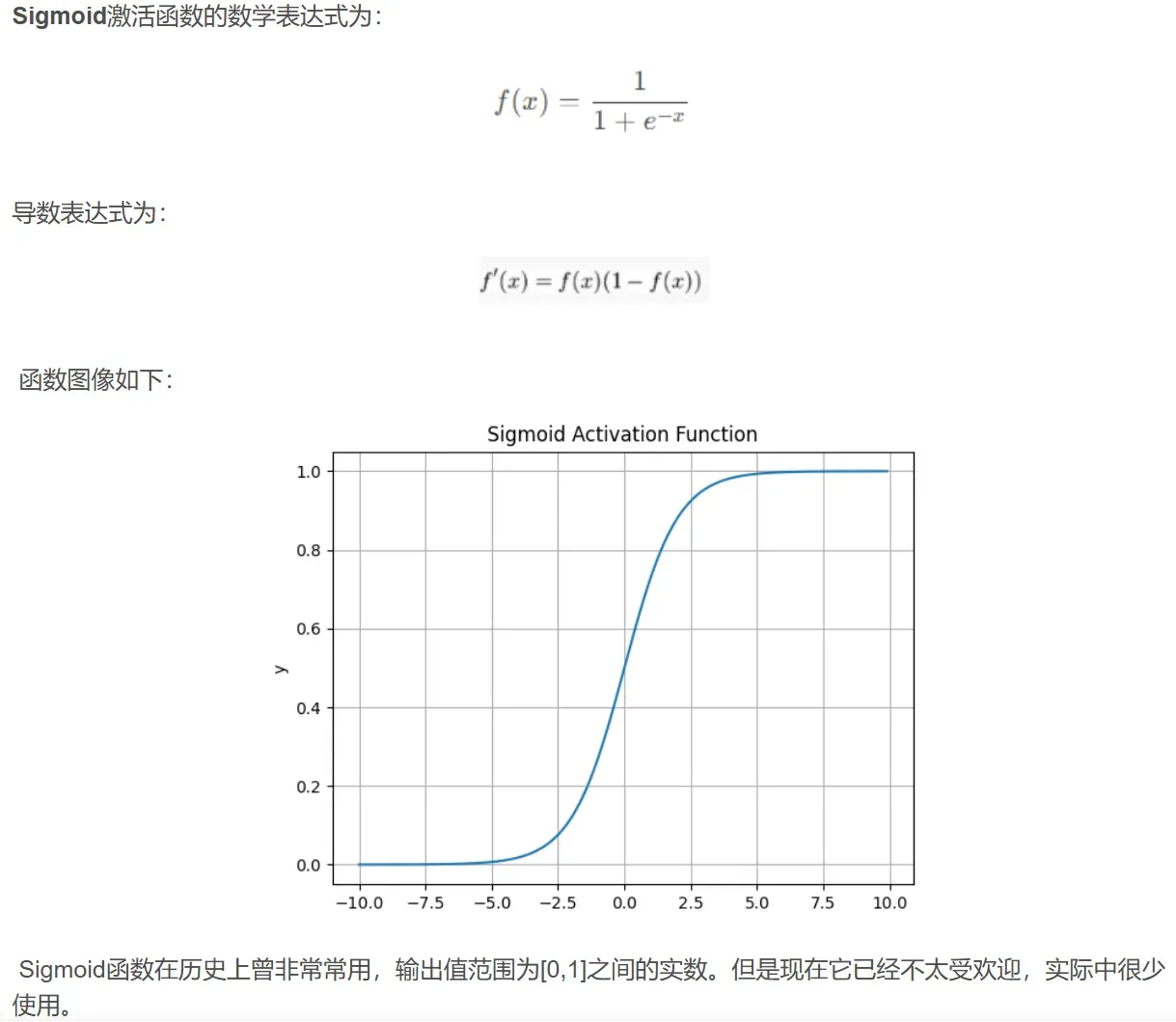
使用激活函数能够给神经元引入非线性因素，使得神经网络可以任意逼近任何非线性函数，使深层神经网络表达能力更加强大，这样神经网络就可以应用到众多的非线性模型中。

论文使用sigmod函数和exponential函数分别得到透明度（因为必须在0-1）和协方差矩阵的缩放（因为必须大于0）

exponential函数：就是对输入进行exp(x)操作

流程#

从伪代码中可以得到如下的简要流程：

获取SfM点云
初始化协方差，颜色，透明度，迭代计数
如果还没有收敛则执行3.x
1. 随机采样一个相机视角 $V$ 和对应的真实照片 $\hat{I}$
2. 利用当前模型光栅化得到一张渲染图 $I$
3. 利用 $\hat{I}$ 和 $I$ 计算得到 $Loss$ 列表
4. Adam优化器用 $\nabla{L}$ 反向传播和参数更新得到新的坐标，协方差，颜色和透明度( $M,S,C,A$ )
5. 当前迭代步数到了特定步数则执行3.5.x
  1. 对于所有的椭球，执行如下两条
  2. 如果透明度太低或者协方差太大则删除椭球
  3. 如果 $\nabla_p L > \tau_p$ $\nabla_{p} L > τ_{p}$ 则执行3.5.3.1
    1. 如果 $\|S\| > \tau_S$ 则split，否则clone
6. 迭代计数自增
完成训练

Structure from Motion#

论文提出的3dgs算法的输入是一组静态场景的照片和对应的通过由2016， Schönberger等提出的SfM算法(COLMAP)标定的相机和得到的点云。

代码仓库中事实上使用convert.py调用了colmap的命令进行图片->点云的转换

SfM算法简要流程#

特征提取：首先从输入的多个图像中提取出特征点，通常使用SIFT、SURF等算法来检测关键点并计算它们的描述子。

特征匹配：对于不同图像之间的特征点，通过匹配它们的描述子来找到对应的点对，建立两两图像之间的对应关系。

三角化：对于至少两幅图像中共享的特征点，利用它们的像素坐标和相机参数，通过三角化算法计算出对应的三维点坐标。

运动估计：通过对匹配的特征点进行运动估计，推断出相机的运动轨迹，即相机的位姿随时间的变化。

结构恢复：同时根据三角化得到的三维点和相机的运动轨迹，恢复出整个场景的三维结构，得到场景中的物体位置和形状信息。

α blend#

论文提到nerf使用的单个像素颜色的合成方法公式为

需要结合采样密度、间距等进行计算

3dgs由于记录了每个椭球体和透明度和椭球体的排序顺序，使得它不用像nerf那样考虑采样因素，而是可以直接按照深度顺序叠加影响像素的椭球体的颜色。

tile-based rasterization#

将整个光栅化过程划分为16*16个tiles，利用多线程并行渲染每个tile，关键在于挑选属于每个tile内部的椭球。论文挑选了99%置信区间的高斯椭球并且拒绝了极端均值（位置），即太靠近近平面和太远离视锥的高斯椭球。将椭球实例化并且通过深度和tile ID分配key值，利用fast GPU Radix Sort对key进行排序。然后每个线程对tile内部的像素进行α-blend渲染。

流程#

从伪代码中可以得到如下的简要流程：

根据相机视角和视锥体选择高斯体
利用相机视角对高斯椭球的位置和协方差进行投影变换
根据渲染分辨率创建tiles
根据tiles和高斯椭球的位置创建key和list
对高斯椭球的key使用快速GPU基数排序进行排序
根据key中表示tile的32位划分属于每个tile的高斯椭球起始位置，得到 $R$
初始化画布
对所有tile，执行8.x
1. 对当前tile中的所有像素执行8.1.x
  1. 从 $R$ 中获取当前tile的起始高斯
  2. 利用像素信息、高斯属性等对当前像素进行α blend
完成光栅化

数值稳定性#

为了避免反向传播过程中可能出现的数值不稳定问题（如除以0），论文采取以下三种措施：

跳过 $α<ϵ$ 的任何混合更新（选择 $ϵ$ 为 $\frac{1}{255}$ ），以避免处理非常小的 $α$ 值
将 $α$ 的最大值限制为0.99
在前向处理的过程中，如果累计的不透明度已经达到0.9999则停止